In this article, our senior contributor E. J. Minnis replies to queries sent in by PPM readers. Please send any questions to: The Editor, PPM, PO Box 551, Dee Why, NSW 2099.
I remember when I bought my first computer, which happened to be a Commodore (where are they nowadays?), and going on a learning curve and buying a few computer books to help the process.
The one thing that struck me was the manner in which the authors wrote their text. It appeared to me that they assumed that their readers would have the same knowledge base of the subject matter as they did.
They were sadly mistaken and that was the main reason why the "idiot" books took off like wildfire with those wanting to easily digest and understand information.
When Max Campbell, who describes himself as a "young punter", asked me "Who makes the odds?" my initial reaction was "what a dumb question".
Then I remembered my early computing days and those awful authors who assumed that the knowledge base of others was as extensive as their own, which coupled with my days as a professional motivator and trainer made me realise that there are no such things as dumb questions.
So who does make the odds?
If by use of the word "odds" we are referring to those available from the TAB operators, then they really are not odds at all - rather the dividends paid out in accordance with the number of winning tickets and collective value in the totalisator pools.
Leaving aside the TAB takeouts and other factors such as the rounding-down effect, if there was a win pool of $100,000 with 20,000 winning $1 tickets, then the dividend would be $5.
Simply put, the dividends paid out by the tote operators are determined by the punters themselves in accordance with how much (collectively) they invest on each runner in a race.
The traditional use of the term "odds" refers to the prices on offer by the bookmakers, but over the past few years they have now changed to "computerised odds" known as "fixed dollar dividends".
The fact that the odds are "made" by bookmakers gives the bookmakers, at least in theory, a big advantage over those who bet with them, as they try to set the odds in such a manner that no matter what the outcome of the event they get a percentage off the top, which can be anywhere between 10 and 25 per cent, on average.
While the odds are heavily weighted in their favour, the least profitable events for the bookmakers are those which work out roughly as expected, i.e. races where the favourites win.
The way that the bookmakers make a "book" is basically a very simple one - they adjust the odds on offer in accordance with the amount wagered on each possible outcome.
The bookmaker is more concerned with predicting the amount that will be wagered on each outcome than in predicting the actual result.
Their job is made easier by the undoubted fact that many punters use the prices as their guide, and perhaps their only guide, to predicting outcomes. This despite the fact that the bookie is not concerned with predicting outcomes but rather with predicting what punters will expect the likely outcome to be.
For those not mathematically inclined, the following concepts may be hard to figure out, but I urge you to persevere if you can.
Suppose that there are three runners and that the amount bet on each (out of 100 units) is Horse A 60 units, Horse B 30 units and Horse C 10 units.
The bookmaker aims to make 15 per cent from the total amount wagered (100 units), no matter which horse wins, so the calculations are as follows:
If A wins, the bookmaker has to pay out: the Odds (Fixed Dollar Dividend) for A x 60 units;
if B wins, he has to pay out the Odds (Fixed Dollar Dividend) for B x 30 units; and
if C wins he has to pay out the Odds (Fixed Dollar Dividend) for C x 10 units.
The total amount taken on the race is 100 units, thus to make 15 per cent his total payout has to equal 85 units (100 minus 15).
Odds for A = 85 divided by 60 $1.40 (which translates to the traditional odds of 2/5).
Odds for B = 85 divided by 30 $2.80 (which translates to the traditional odds of 7/4).
Odds for C = 85 divided by 10 $8.50 (which translates to the traditional odds of 15 / 2).
In fact, if either A or B wins, then the bookmaker would pay out only $84, so he would make an extra one unit profit on the race.
The 15 per cent that the bookmaker makes is directly related to a quantity called the "overround" on that particular race. The "overround" on any given race can be obtained by converting the odds (fixed dollar dividends) to a percentage, then summing those percentages.
For example, the "overround" on the above example is:
A (100 divided by 1.40) = 71.4%
B (100 divided by 2.80) = 35.7%
C (100 divided by 8.50) = 11.8%
Total: 118.9%, an "overround" of 18.970.
The same process can be applied to totalisator pools, which would disclose similar "overrounds". However, the difference between the TAB operators and the bookmakers is that the bookies can (and do) lose on some races - the TAB operators never do.
Marcus Beeble of Melbourne contacted me with some follow-up questions re my response about the Oscar's Grind staking plan in the March 2003 issue of PPM.
The following is an extract of his email:
"Thanks very much for your answer to my earlier query about place punting. In some ways your answer begs more questions and I would like you to clarify a few points.
Oscar's Grind looks a promising staking method, but I notice that in the simulation you published the winners came in batches. But what happens if this doesn't happen? What happens if the winners and losers come in sequences like WLWLWLWLWL?
In the simulation only a $2 (even money) dividend was used. What happens when the dividends are less? For example, in the last two years I've had 316 selections for 232 winning bets at an average price of $1.50, which has given me a profit of about 10 per cent.
How should the staking plan be operated in this case?
Where strike rates are in excess of 50 per cent, in most instances the winners will tend to come in batches, while with selections that average less than 50 per cent it tends to be the losers that will occur in batches more often than the batching of the winning selections.
Statistically, with the strike rate (73.4 per cent) that you are achieving, the long-term expectation is that there will be at least one losing run of five in each 1000 bets, but only a one-in-five chance that there will be a losing run of six or longer.
Conversely, if the results that you supplied me with held up for a long time, then in each 1000 selections there should be approximately 105 occurrences of the winners coming in batches of three or more.
In examining the use of Oscar's Grind as a suitable staking plan, I was aware of the fact that to operate at an optimum level, batches of winners would be necessary as any sequences similar to the one you mentioned of W-L-W-L-W-L etc. would not only be very frustrating but be unsuitable for the long-term success of the staking plan.
When operating the plan on selections with an average winning dividend less than $2, then rule 3 needs to be amended to the following:
Rule 3: After a win, the next bet is one unit more than the previous one, so long as the dividend is $2 or more. Where the dividend is less than $1.50, the next bet should be the same size as the previous one, while if the dividend is between $1.50 and $1.95, then the next bet should be increased by the amount of the percentage profit of the base bet, i.e. a winning bet that returned a dividend of $1.60 would mean an increase of $6 (assuming a $10 base bet) on the previous bet. (Note: The other rules remain as previously published.)
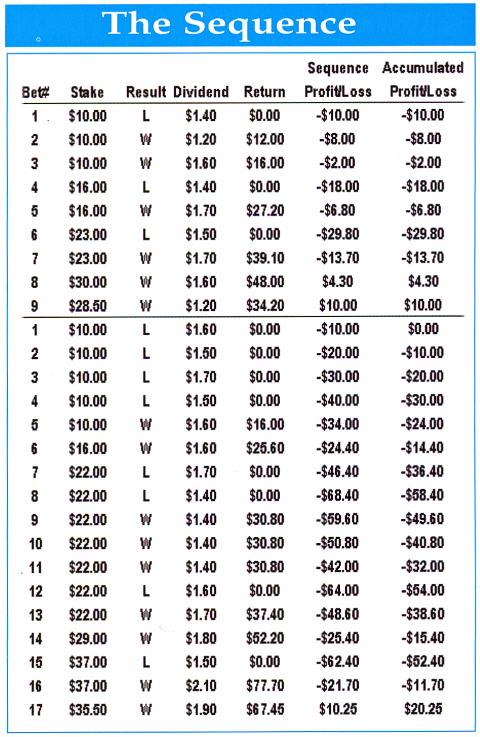
I've taken a slice of 26 of your selections, not a particularly good sequence as the strike rate of 57.7 per cent is well below par, showing a loss at level stakes of 8 per cent.
Oscar's Grind manages to turn that around into a profit of just under 4 per cent but this sequence displays the stresses the staking plan can come under when the selections are not performing, as well as demonstrating how the revised rule 3 handles selections that return dividends less than the $2 threshold.
By E.J. Minnis
PRACTICAL PUNTING - JULY 2003