Many people refuse ever to bet eachway, arguing that in the long run you will be further ahead (or less far behind) by sticking to straight-out bets.
The main argument against place betting, and therefore against each-way betting, is that it is poor value. You have three chances of collecting instead of only one, but you get only one quarter of the odds. In races with fewer than eight starters this discrepancy seems even more marked; you collect if your horse runs first or second, but the odds offered are only one third of the win quote.
It may seem as if you should get one third of the straight-out price if there are eight or more runners; in fact in most situations the correct odds lie somewhere between one third and one quarter of the straight-out quote.
Consider the hypothetical case of a race in which there are nine evenly matched runners. The theoretical probability of any given horse's winning is 1/9, i.e. odds of 8-1.
The probability that that horse runs a place is three times 1/9, i.e. 1/3, or odds of 2-1.
So in this case, a quarter of the odds is theoretically correct. For eight evenly matched horses, the theoretical place odds are slightly less than one quarter of the win odds; but as the number of runners increases, the theoretical odds become increasingly greater than one quarter of the straight-out odds, although they never get as high as one third.
For instance, in a field of 24 starters (which occasionally occurs in sprint races at Flemington), hypothetical win odds of 23-1 should give rise to place odds of 7-1-very nearly one third.
But these hypothetical fields, with evenly matched horses, do not occur in practice, and we are concerned with practical punting. It is, however, possible to modify these theories to more realistic situations and to apply them on-course. I stress 'on-course' because it is in the realm of place and each-way betting that the on-course punter enjoys the greatest advantage over the stay-at-home TAB punter.
Consider the still hypothetical, but more realistic, situation in which five horses can be conceded a winning chance, and the remaining runners are at long odds. In the eyes of punters and bookmakers, each of these five may have a probability of winning of l/s, and be quoted at 4-1. The outsiders provide the bookie with his profit margin.
If you ignore the outsiders, and consider your selection to have a probability of winning of 1/5, his chance of running a place is Vs, equivalent to odds of 6-4 ON. But by backing him each way at 4-1 you are getting even money for your place bet. Of course an outsider can still get up, or nudge you out of a place, but this does not alter the fact that the place portion of your each-way bet is good value-better value than the straight-out portion. This, then, is a situation where you could reasonably bet each-way.
Why not just back your selection for a place? Because you won't be offered even money. A straight-out bookmaker can hold the necessary 100 on five horses each at 4-1; but the same five horses at evens the place will bring in only 250 for a place bookie instead of the 300 he needs to balance his book. He can only afford to offer you 6-4 ON. Similarly the place tote will be offering an average return of only 83 cents (rounded down to 80 cents), assuming again that investments on the outsiders provide the tote with its profit margin.
Despite this, you probably won't have much difficulty in obtaining 4-1 each-way if you shop around-4-1 the field would be described as an open race by many people, and one on which plenty of bookmakers would be operating each way.
The 'win-only' signs go up all through the ring when the favourite is odds-on, or near it. Any fielder displaying an 'eachway' sign will be offering more cramped odds about those runners other than the favourite-but in the circumstances an each-way bet at a lower price may provide better value than a straight-out bet on the same horse. The further the favourite is into the red, the more pronounced may be this advantage.
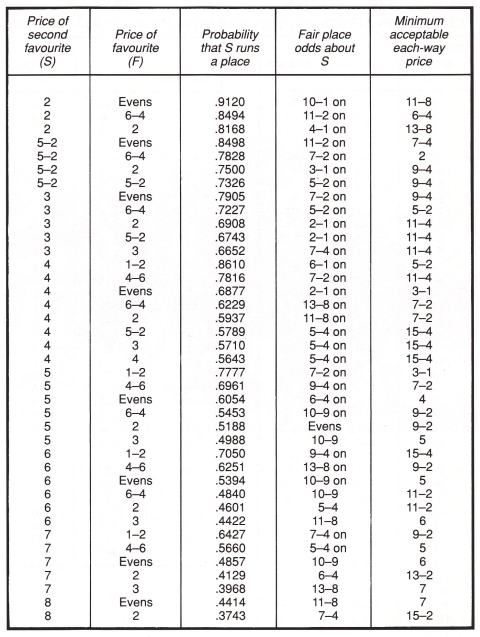
Let's consider a race (with eight or more runners) in which the favourite (F) is quoted at evens; you think it will probably win, but you're not prepared to accept the odds, and you think that your selection (S) offers better value at 5-1. The best you can see each-way, however, is 4-1, and of course the place bookies and the tote have S at 2-1 ON the place. What should be the theoretical odds about S for a place?
The arithmetic gets a bit complicated, but in fact 6-4 ON is a reasonable price to accept for the place.
Now which is the better bet-5-1 straight-out, or 4-1 each-way? Let's say you were going to have $8 on at 5s, to give you a profit of $40 if S won. Instead, have $10 each-way at 4s. You can think of this as two separate bets: a win bet at 4-1 to give a profit of $40, and a place bet at evens to give a profit of $10.
As a direct comparison with the straight-out bet, your $20 investment can be considered as $8 for the win, to give a profit of $40; and $12 for the place, to give a profit of $10. By considering the bet in this way, you are still getting 5-1 about your win bet, and in addition taking a place bet of $12 to $10 ON (odds of 6 to 5 ON), when the correct odds are 6-4 ON.
So in this case, 4-1 each-way is better value than 5-1 straight-out.
Even if you can't find 4-1 each-way, 7-2 each-way is still theoretically a fair bet: $14 straight-out would win $70 at 5-1 * $20 each-way at 7-2 gives you a profit of $70 for the win, and $17.50 for the place.
The extra $26 invested for a place profit of $17.50 represents odds of almost exactly 6-4 ON.
This may be a suitable point for discussing each-way bets at less than 4-1 Many punters, perhaps the majority, will not consider an each-way bet unless they are offered 4-1-so-called each-way odds. Their reasoning is understandable; a 'winning' bet at 3-1 each-way will result in your losing money if the horse runs second or third.
Other punters take this reasoning a stage further, and don't bet each-way unless the bet will show a profit if the horse runs a place. They won't take 4-1 each-way, and may have a personal rule limiting each-way betting to horses at 6-1 or longer, or 8-1 or longer.
Such a view is rather short-sighted, as I think has been shown by the example we have just considered. Several professional punters I have talked to go to the opposite extreme, making something of a speciality of backing selected favourites each-way at prices of 2-1 and even shorter.
The type of situation where this applies is one in which you think the favourite can win, but there is one logical danger or at most two other horses which can be given a real chance of winning. This most usually occurs in restricted class races at provincial meetings, but occasionally similar situations crop up in the city.
The two 'dangers' might be around 4-1, with double-figure odds available about the rest of the field. Backing the favourite at 2-1 each-way gives you odds of 2-1 ON for the place, when you think it is a near certainty to run a place.
Instead of risking $100 straight-out at 2-1, with a chance of winning $200, the pro might take $400 to $200 each-way. If the horse is beaten, but runs a place, he still loses $100 ($300 return for a $400 outlay). But if it wins, he makes a profit of $500.
Occasionally, of course, the favourite will run out of a place, resulting in a $400 loss; but this rare occurrence is more than compensated for in the long run by the extra profits. Clearly the same reasoning can be applied to a bet of $10 or even less.
It is usually not difficult to get set eachway on the favourite in such a race. Eachway bookmakers may have the logical dangers at 7-2 instead of 4-1, but so few punters will want to back the favourite each-way that it is unlikely to be shorter with the 'win-and-place' than with the 'win-only' bookies.
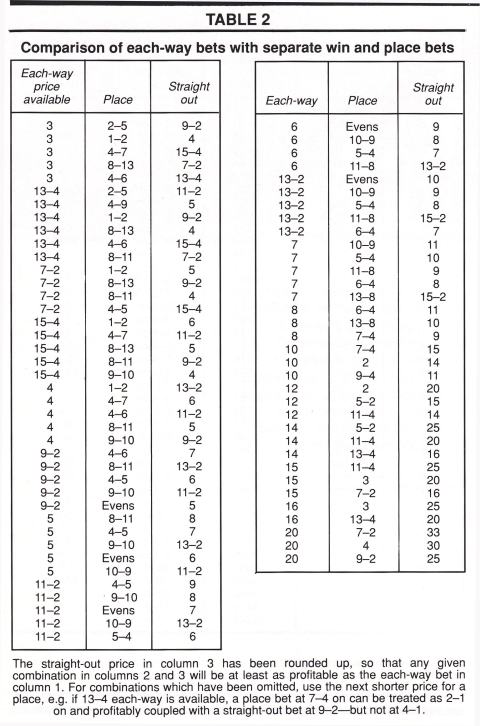
The straight-out price in column 3 has been rounded up, so that any given combination in columns 2 and 3 will be at least as profitable as the each-way bet in column 1. For combinations which have been omitted, use the next shorter price for a place, eg. If 13-4 each-way is available, a place bet at 7-4 on can be treated as 2-1 on and profitability coupled with a straight-out bet at 9-2 but not at 4-1.
Click here to read
Part 1.
By Roger Dedman
PRACTICAL PUNTING - MARCH 1988