Most serious punters who are totally committed to winning have at some stage of their betting lives made a price line where each horse has been allotted a price commensurate to its chance of winning the race.
If the assessor felt a particular horse could win this race one time out of three attempts the horse was allotted the price of 2/1 and if its chance was one in five it was allotted 4/1. (Don’t panic I will explain shortly how this is worked out.)
In order to be able to price a field sensibly the assessor must know the percentages of horseracing and I must admit it amazes me to note how many punters, many of whom are adept at horse race betting, still do not know how to calculate percentages. In order to help newbie punters to learn this “must know” facet of horseracing I will start with the simplest of calculations and build up accordingly.
Life as a punter in the early, early days of the punt, when the various lords of the time in Ye Olde England raced their best horses against one another, was a simple case of mine versus yours. In this situation, each owner had a chance of winning and a chance of losing and like the toss of a coin the odds for both were 1/1 or 50/50, thus the percentages were 50 per cent for each horse which total 100 per cent.
The mathematics of it all became more complex when three lords decided to race their respective steeds. In this instance each owner has one chance of winning and two chances of his horse being beaten; thus the odds for each runner became 2/1. If you add the two and one of 2/1 you get three and if you divide three into 100 per cent you get 33.33 per cent which are the percentage chances of each runner. The punter who knows both the odds AND the percentages knows that 2/1 equals 33.33 per cent.
The above simple scenario assumes all three runners have an equal chance of winning. However, let’s say one of the horses may have raced against one of today’s other two runners and just been beaten one length. For the sake of this explanation let’s assume the other two runners have met one another and dead heated for first and therefore neither is better than the other.
This is the first sniff of what a price assessor/punter would call a formline. If you, as the punter, wanted to have a bet you would be foolish to accept the same odds on the horse that had been beaten as the other two horses. This is just plain old commonsense and no knowledge of percentages is needed and nor would this punter not know that the odds of the beaten horse needs to be extended to longer than 2/1. If there was only one length the difference perhaps the truer odds for the beaten horse should be 3/1.
If we add the three and one of 3/1 together we get four and if we divide four into 100 per cent we get 25 per cent as the percentage of a 3/1 chance. If the total percentage for the event is 100 per cent and if the two remaining runners are equal in chance based on their dead heat then the total odds for the two must total 75 per cent (100-25) with each receiving 37.5 per cent as their share of 75 per cent.
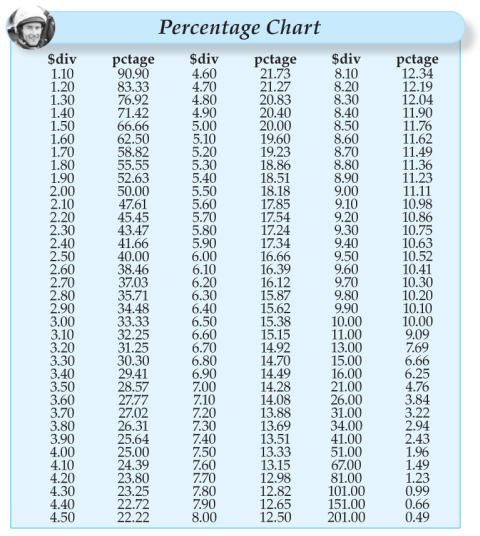
In the Percentage Chart with this article, you will note 37.5 per cent is around $2.70, as most would know it from the TAB screens or in the olden days at 7/4. This is not exact because of the fractions involved but I am sure you get the big picture which is more important than worrying about miniscule decimal points.
Before any adjustments for the “form line” mentioned Horses A,B and C were all 33.33 per cent chances of winning which, when you refer to the PC Chart, is $3.00 on the TAB screens. However, once the “form line” was introduced the odds for this race would have become Horse A at $2.70, Horse B at $2.70 and Horse C at $4.00.
It doesn’t take a rocket scientist to assess the odds if there were 10 runners in a race where the chances of all were equal because each horse mathematically has one chance in ten of winning (10 per cent) which on your TAB screens is $10, while we oldies also know it as 9/1. Naturally, we all know that each horse does not have an equal chance of winning and form adjustments need to be made to the odds so that if there are 10 punters and each of the punters backs a different horse they all receive fair odds.
From this point the life of the punter who wants to become a price assessor becomes more complicated than the scenarios I have set out. In order for the newbie punter to understand what needs to occur before a sensible price line can be set is to peruse the Percentage Chart.
This chart is just a listing of the TAB odds and their relative percentages. The percentages are simply calculated by dividing the TAB price into 100 per cent and the resultant figure is just simply the percentage for that horse’s chance of winning. There is however a problem attached to the simple examples I have given you so far.
All of what I have written is based on the percentages of all runners totalling 100 per cent but if you added up the percentages on your TAB screen you would find the percentage total for all runners would be about 114 per cent.
If the TAB odds added up to 100 per cent the TAB would make no profit as they would have punters betting $100 and then have to pay them back $100; hence the TAB screen odds are programmed to about 114 per cent. This means that for every $114 they receive from the punter they payout $100 with their profit $14 or 14 per cent.
How they do this is quite simple. For every dollar put over the counter the TAB program immediately deducts 14c and then “puts” the remaining $0.86c into what is called the betting pool and the number of winning tickets on the winner is divided into the total pool (all the $0.86c amounts) to provide the punter with whatever dividend the horse pays.
It will not surprise you to know that the bookmakers also work on a similar principle. However, because they have certain overheads they have to meet each meeting, they must have certain percentages they need to work to. If there are 10,000 punters at a meeting the passing trade may allow a bookmaker to operate at 110 per cent (pays out $100 for every $110 bet by punters) and actually be competitive with the TAB.
Overall, though, if there are only 1,000 punters then the bookmaker may have to operate at 120 per cent (pays out $100 for every $120 bet by punters) to cover expenses. At this stage let’s not worry about the bookmakers because we want to learn how to combat them in the way they fear the most, which is when punters make their own odds line.
All bookmakers love the mug money of ill-informed punters because they can give the mugs any price and the mugs lap it up without thinking. However, if all the punters at the track were punters who did their own prices solely based on form opinions the bookmakers would be literally terrified. (Well, maybe not terrified but extremely cautious!)
Any discussion like this, about making price lines, needs to start with the doyen of Australian price assessors, the late Don Scott, who started a punting revolution in 1979 when he published the first of his trilogy of punting books, called Winning.
Three years later the thin initial volume had been massively expanded when he published The Winning Way and, voila, a new breed of punter was born . . . punters who were very, very price conscious. The revelations Don imparted to his readers were extraordinary and to read how he went about the business of winning on the punt is still compulsive reading for any punter who wishes to attack the punt with some real seriousness.
In his books Don Scott espoused the concept that punters should make a price line that added up to 80 per cent, which is quite a percentage difference from the 100 per cent mentioned earlier when the aristocracy raced against one another all those years ago and is a 50 per cent difference to the 1,000 punters racetrack scenario I mentioned earlier. By pricing to 80 per cent Scott maintained the difference in percentages gave the punter a buffer against the odds set by the bookmakers and if you could price horses accurately in the long term you would be only backing value runners.
If we pop back to our very first example, that of the two runners of equal ability, I hopefully can show you how you should be looking at the pricing of horses as I up the ante in the difficulty stakes.
In the two horse example, if you backed both of the runners at 1/1 to return $100 you would have $50 on Horse A and $50 on Horse B and whichever won you would win $50 plus receive your $50 bet back on the winner as well totaling $100 for no profit at all.
If, however, for some weird reason you could receive 6/4 ($2.50 at the TAB) for BOTH runners your outlay on each would be $40 ($100 divided by $2.50) totaling $80 and no matter which horse won you would win $20.
Broadly speaking this is the premise Don Scott worked on which was for every $80 he outlaid he wanted to receive back $100. This is playing the bookmaker at his own game. In the reality of the horseracing scene as we know it this was not possible every time because, as we shall see, by pricing horses to a percentage of 80 per cent versus the bookmaker at 110 per cent – 20 per cent would mean our prices must be longer.
This makes sense if we have just two horses of equal ability in an 80 per cent field then we can only have them at 40 per cent ($2.50) while the bookmaker betting to 110 per cent would have them at 55 per cent ($1.80 approx).
If our prices are longer overall then in some instances we will have priced some horses as better chances than what the bookmakers have them i.e. bookmaker has 5/1, we think 3/1= value for us if it wins and in other instances we will have priced some horses as longer i.e. bookmaker 3/1, we think 5/1 = no value for us.
Due to this mish mash of opinion between ourselves and the bookmakers it means there will be races where we miss out on the winner simply because we have assessed the winner’s chances incorrectly. However, the Don Scott theory of value says if we back enough winners at odds equal to or higher than our assessment then we will win overall.
In the next issue of PPM I will detail what happens if you decide to price your chances to as low as 50 per cent and as high as 110 per cent. The aim of that article will be to have you decide just how tight or how loose you want to be when betting to your assessments.
Until then, good luck.
Click here to read Part 2.
By Roman Kozlovski
PRACTICAL PUNTING – AUGUST 2008