There is less than a minute to go before the jump. What to do? Win bet? Exacta? Trifecta? How much on each? What's right?
While the questions posed seem simple, they are problems that mathematicians and gambling experts have debated for centuries. They encompass many elements.
Boil it down to these:
- If I am a winning punter, how can I maximise my wins while maintaining a playable bankroll during a losing period?
- If I am a losing punter, how can I minimise my losses while maintaining a playable bankroll, and still have a chance to win?
It may not be totally solvable for horse-racing punters, even in these days of high-speed computer simulations. Even our definitions are problematical. IS your "bankroll" what you take to the track on a particular day, or your total stake? If you lose your entire gambling
bankroll, can you raise another one?
Virtually all games of chance are "fixed negative-expectation games". A certain house-edge is built into the game. This edge cannot be overcome by any money management strategies.
No matter what you do at a roulette table, for instance, the house edge is 5.26 per cent. Bet the player's hand in baccarat and you're bucking a 1.23 per cent disadvantage. This is why there are no professional roulette or baccarat players.
Horse-racing betting, while it suffers from a large house-edge, can be either negative or positive, depending on the bettor. Punters wager against each other, not the house. The crowd's collective bets determine the odds.
A punter has the choice to accept the offered odds, or not. If he feels that the horse should be 2/1 but the crowd makes him 3/1, he'd bet.
Thus, by being selective and betting only on horses he perceives to be bargains, a punter might be able to overcome the house edge and
win.
I say "might" because it is possible to reduce the house edge by good selecting and betting, yet still lose. A punter who bets $100,000 and gets back $90,000 has beaten the house edge (takeout and breakage) but still loses.
Determining whether a punter can be a long-term winning or losing bettor at horse-racing betting is far more difficult than it is in games such as baccarat or blackjack. These near break-even games reward winners with $1 for a win and take away $1 for a loss, with minor exceptions (such as doubling and splitting at blackjack).
Because no individual hand makes much of a difference in the long run, it is simple to run computer simulations of thousands, or even billions, of hands using particular strategies.
And because the games themselves are fast paced (a blackjack player playing head-up against a dealer, or at an Internet casino, can easily play 200 hands per hour) the long run is easily reached.
Not so for horse-racing betting. A blackjack player who bets for 10 hours one weekend a month, betting 75 hands per hour, will bet 39,000 hands in a single year. A horse punter who bets 10 races each weekend will bet only 520 races in a year, a number so pitifully small that the result of a single race or two might determine whether the year ends with a profit or a loss, especially because payoffs vary so widely.
Even punters who bet strictly to win (are there any of these left?) might bet a 2/1 shot in one race and a 20/1 shot in the next. If they bet the same amount on each race, the longshot's result counts ten times as much towards the year's bottom line.
Bettors who put most of their money into such wagers as trifectas or Pick 6s (and Pick 4s, etc.) have swings so wide as to make computer simulations impractical because no mortal will ever live long enough to get into the long run.
The essential strategy in any gambling game must consider BOLDNESS, defined as how big a bet you should make. In a positive expectation game, use minimum boldness, since the longer the run of results, the more likely you are to wind up ahead.
In a negative-expectation game, though, better to use maximum boldness, since the more rounds you play, the more likely you are to wind up behind.
Therefore, given equal $1000 bankrolls, long-term losing punters would be better served by betting the whole thing on one race and hope to get lucky (then quit the game forever), while long-term winning punters are more likely to wind up ahead with 500 bets of $2 each.
However, to be able to stay long in a negative-expectation game (which horse-race betting is for most punters), you should NOT be using maximum boldness. Instead, you need a large bankroll and small bets. Eventually, you will be ground down to defeat, but you may have a
heck of a lotta fun getting there.
This brings us to the question of short-term versus long-term strategies. A betting strategy that will probably be successful for a short period (for instance, double your bet on every favourite, then quit after one wins) is usually doomed to failure in the long run. Any strategy we devise should be based on the long-term, not the short-term.
The strategy should also make preservation of capital a priority. If you hit 99 per cent winners but bet 100 per cent of your money on every race, eventually you'll hit a loser and tap out. And nobody hits 99 per cent winners. So you have to bet only some small fraction of your capital, no matter how good a horse looks.
The strategy also has to relate to your perceived edge on the bet. Naturally, if you believe there's no edge, there's no point in betting. But as your edge increases, so should your bet as well.
For instance, it's reasonable that if you make a horse 2/1, you bet some amount if he's at 3/1, and some higher amount if he's 4/1. However, this is tricky because there will be races in which you THINK you have an edge but you don't.
Overbetting can easily lead to bankruptcy. Nonetheless, there should be some provision in your plan for increasing your bet when you have a higher edge.
The strategy also has to allow for the fact that horses with high odds win less frequently than horses with low odds. Therefore, your losing streaks will be longer with longshots, so you'll either need a larger bank, or smaller bet sizes, to play longshots.
The same is true, but on a more pronounced scale, once you get into low-probability bets such as superfectas or Pick 6s. It is quite possible to play a $200 Pick 6 (or a similar Australian bet) for an entire year and wind up with only a few small hits and some teasing
5s.
If you're betting $1000 Pick 6s, the situation can be much, much worse, even though you'll doubtless hit more often.
Let's talk for a moment about expectation. You can also call it the expected value or the edge. It is simply the percentage value of a particular play.
This can be calculated in games with fixed edges, but can usually only be estimated in horse-racing. You make a horse a certain price, the crowd makes him a different price. Thus: edge.
Even with an edge, it is possible to go broke if your bank cannot handle the volatility of the results. For instance, take a lottery which gives away a mandatory $1 million to a single player but attracts only $740,000 in bets. The expectation is a strong $1.35 per $1, a 35 per cent edge.
However, despite this huge edge, the bank needed to participate in such a game makes it not particularly attractive. A player betting $1 could easily lose $1.5 million before hitting the lucky number. Thus, the expected value of the bet, while important, is not the only element
in our decision.
How often a bet wins is significant. The conclusion: You cannot bet the same amount on longshots as you do on favourites, even with a higher edge.
The betting method that addresses many of these concerns is the Kelly Criterion (the original paper, published in the Bell Technical Journal in 1956, is available for download from the Internet at www.bjmath.com), which recommends you bet a fraction of your bankroll this way:
EDGE DIVIDED BY ODDS: For instance, with a 20 per cent perceived edge, you'd bet this percentage of your bankroll: 16.7 per cent on a 6/5 shot, 5 per cent on a 4/1 shot, 1.1 per cent on an 18/1 shot.
The essential problems with using the Kelly Criterion at the racetrack are that your edge is always PERCEIVED rather than EXACT (you may simply have mishandicapped the race) and that the Kelly percentages are far too high for horse-race betting.
Nevertheless, the idea to make smaller bets on longshots is a sound one, even though most punters would rather send it in on a 12/1 shot than a 6/4 shot since, hey, score time if you're right.
A simple method proposed by Stanford Wong in Betting Cheap Claimers doesn't require that a player even know his edge at all. Wong suggests setting a target amount per race, then betting whatever amount is necessary to reach that target depending on the odds.
So if your target is $100, you'd bet $50 on a 2/1 shot but just $10 on a 10/1 shot.
This method differs from the duecolumn method which attempts to recoup previous losses by setting targets. With Wong's method you're forced to correctly bet more on horses that are more likely to win, yet you don't chase losses.
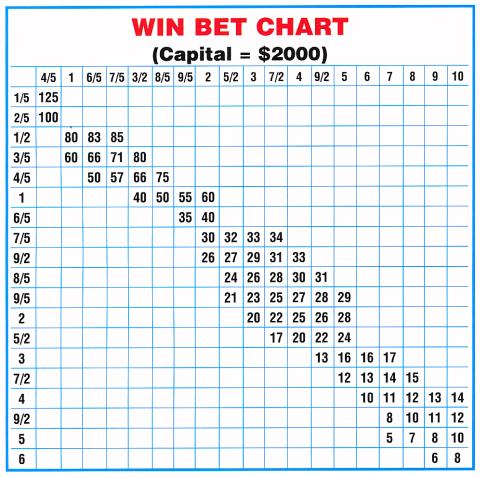
In my book Money Secrets At The Racetrack, I created a chart (see below) based on several aspects of correct money management betting MORE with a higher perceived edge, betting less as the odds are higher, and betting a small enough proportion of your bankroll to be able to maintain it even during bad streaks.
The chart, for a $2000 win-bet bankroll (this can be raised or lowered depending on your own circumstances), ensures that even if you have a bad day, you'll be around to bet another day.
The numbers to the left represent your odds for the race, while the numbers on the top represent the tote odds (or bookmaker's odds). If you make a horse 9/5 and he goes off at 5/2, for instance, you'd bet $21 on him. If he goes off at 3/1, you'd raise your bet to $23.
Any horse going off at higher than the maximum odds on the chart (e.g., a 3/1 shot on your line who goes off at 8/1 or higher) should be bet the maximum number listed (in this case $17).
You can safely bet higher amounts to place because you'll collect on these more often than you will on win bets.
This article contains extracts from a larger article in Barry Meadow's popular Racing Monthly newsletter. Details from TR Publishing (www.trpublishing.com).
By Barry Meadow
PRACTICAL PUNTING - JANUARY 2003