Special Report
The late Eric Connolly, one of the great punters in his heyday, always maintained that the key factor in betting was obtaining VALUE, and that every punter should know all about the meaning of odds.
He said: "When punters start dual betting, and making savers, they seldom realise the short odds they sometimes accept." To illuminate his point, Connolly pointed to the punters who backed the first two favourites in a race.
"Assuming that the first favourite is 2/1 and the second favourite is 4/1, do you ealise what price this is that either one won't win? The punter is actually laying 8 to 7 ON." It's easy to do a workout to discover facts like this. You invest $1 each on the first two favourites (total outlay $2). If the favourite wins you collect $3, including the $2 invested. So you have actually laid 2 to 1 ON. Should the second favourite win (4/1) you collect $5, which includes the stake of $2. So your overall price on the 4/1 winner is only 6/4.
To work out any problem in multiple betting you have to add the odds to 1 to each bet and then add the least common multiple.
Example:
First Bet, the price was 2/1. Add 2 and 1 and you get 3.
Second Bet, the price was 4/1. Add 4 and 1 and you get 5.
The least common multiple of 3 and 5 is 15, so the odds that one or the other does NOT win are 8/7 ON. You'll have to be a very sharp, shrewd and agile punter to win with figures like this!
Let's now look at a race where three horses are backed. Bay is 3/1, Grey is 7/2 and Chestnut is 9/1. Now, 3/1 is represented by placing four balls in a bag-three of them black and one of them white. The price 7/2 means nine balls in the same bag, seven being black and two white. Finally, 9/1 means 10 more balls in the bag, nine of them black and one of them white (total of 19 black and four white).
The lowest common multiple of 4, 9 and 10 is 180. So the combined chances about one of the three winning equals the drawing of a white ball from a bag containing 180 balls, of which 103 are white. Therefore, the multiple odds you have accepted against any one of your three horses winning is 103 to 77, approximately 4 to 3.
Thus:
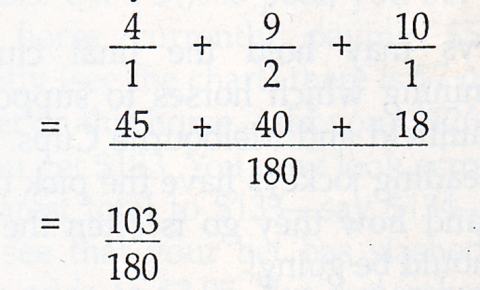
Presuming you accept the odds to $1 about each of the three, you will collect $4 from a total investment of $3 if Bay wins, $4.50 if Grey wins and $10 if Chestnut wins. The respective odds represent 3/1 ON, 2/1 ON and 7/3 against. So, the lesson is that multiple punters should watch the odds very closely and bet only after much calculation. Essential in this form of betting is the compiling of a tabulated price schedule so you can instantly realise what odds you are accepting about the number of runners you have decided to back.
Go up from the simple priced favourites to a multiplicity of them. Start by noting that 3/1 against two equal favourites is not 3/2 but even money (four back for outlay of two). Also, 8/1 against three runners taken separately means 2/1 against any of the trio winning. Get that? Although you've backed three horses at 8/1 each you really are only getting 2/1 should one of them win. You have bet a total of $3 but the most you can get back is $9-so that's 2/1 for the actual $3 outlaid.
If anything, what all this points up very clearly is what an infallible position the bookmaker is in. It also underlines the great importance of care and attention to detail in multiple betting. The slogan is 'small profits, quick return’. This is because, as pointed out, even backing three horses at long odds will shorten the price considerably.
Example: You back three horses each at 12/1, for $1 each. Your maximum return is $13. Thus, should one of them win you are, in fact, getting a $13 return for a $3 bet, odds of just over 3/1. So much for your 12/1 odds!
Despite all this disconcerting analysis, multiple betting is SAFE, provided you are clever enough to strike a big average of winners. The secret to cope with what I call the 'many moods' of multiple betting is going for a big stake on your first choice and then merely covering your losses with a slight interest percentage, or a saver on the other fancies.
Let's look again at those three horses mentioned previously-Bay 3/1, Grey 7/2 and Chestnut 9/1. What if you had decided to adopt the Eric Connolly approach of going for a win on one of these horses and saving the stake on the other two? The formula for doing this is to add one to each price and then divide that sum into the total stake to discover how much to invest on your 'savers' with the balance being placed on the main choice.
This is a good method-providing you concentrate on races which will enable you to pick a high percentage of winners! In the case of Bay, Grey and Chestnut, let's say you decided to go all out for Bay to win, and save on the others. Your betting bank is $50. Therefore, you would have $11 on Grey, and $5 on Chestnut, leaving you $34 to place on Bay at 3/1. If Bay wins, you get back a total of $136 for a profit overall of $86. If Grey won, you would get back $49.50, and cover your bet save for 50c. If Chestnut won, you would get back $50 for a complete 'save' on the bet.
The actual price achieved about the 3/1 winner is 7/4 (i.e., $50 wins you. $86, odds of 1.72 to 1). But, think about it: You have made a tidy profit without a great deal of risk. By sacrificing that 1.25 points of the 3/1 price, you have been given the 'insurance' of having two other horses racing around to 'save' your stake for you. So there is a price to be paid for the multiple, and the price you pay is the reduced odds about the winner. So be it.
Of those people who go racing regularly-to the track, that is-the two groups which do best financially are the professional punters and the bookmakers. They share the money lost by the 'gamblers' and that section of the huge punting public which sets out to back every winner (and fails, of course).
There have been very few professionals, though, who have beaten the bookmakers by betting just one horse per race. The one horse a race pro has to be someone of extraordinary patience, will power and courage. Lesser patience, willpower and courage are needed by the punter who doesn't mind taking a smaller profit for the insurance of having saver bets on his side!
Now we'll run through the mathematics of simple multiple betting: In the first example, A is 3/1, B is 7/2 and C is 5/1, and we want to invest $10 and win the same amount on each horse. The total sum of their 'chances' equals .639 (3/1 is .250, 7/2 is .299 and 5/1 is .167, refer to our odds percentage chart). Thus the workout goes as follows:
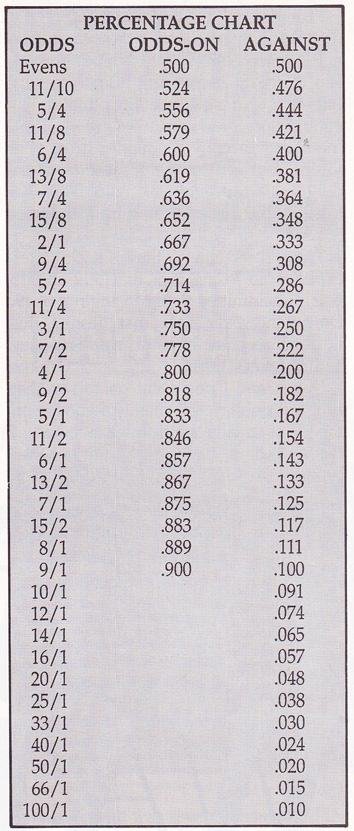
Whichever horse wins, we get a return of at least $15+. In reality, you would have to round off the stakes to $4, $3.50 and $2.50.
This manipulation of stakes can be done in a variety of ways. Suppose, using the $10, we wanted A and B to return the same profit, whichever wins, and have a saver on C? We take the saver bet first so the stake on C is $1.67, leaving us $8.33 to be divided between A and B. The probability of A is .250 and B is .222, which total .472.
So, if A or B wins you have a profit of $7.64. If C wins, you break even. Again, you would have to round off the bets to $4.50, $4 and $2. In these examples, three horses have been used but the principle is the same for any number of horses. The only thing to watch out for is the total of the probabilities. If it is less than ONE then you can bet and make a profit; if it is more than ONE you cannot bet on all the runners and show a profit whichever wins.
Here's another way you can do a multiple bet quite easily. Let's say you come to a race where you decide to save on Black, White and Grey and go for an equal win on Roan or Red. The prices are: 3/1 Roan; 9/2, Red; 4/1, Black; 8/1, White; 9/1, Grey.
The quickest formula-as already explained-to arrive at the mount of the insurance bets is to add ONE to the price and divide into the total amount to be bet. Let's say the total bet is to be $100. To find the bet on Black at 4/1 we divide 5 into 100 and the result is $20. On White we divide 9 into 100 and get $11, while on Grey at 9/1 we divide 10 into 100 and get $10. Our 'book' now reads: $80/20 Black, $88/11 White and $90/10 Grey, a total of $41, leaving us $59 to be placed on Roan and Red in such a way as to return the same amount whichever one wins.
Now, Roan at 3/1 has a chance of .250 while the figure for Red at 9/2 is .182. This is a total of .432, so our bets will be:
Roan-$59 multiplied by 250, divided by 432.
Red-$59 multiplied by 182, divided by 432. To the nearest dollar bet, this would be $34 on Roan and $25 on Red, the actual bets being: Roan, $102/34; Red, $112/25.
The total investment, then, is $41 on savers and $59 on the win bets. A win by any of the savers will square the bet but a win by Roan or Red will bring in around $136 for a profit on the entire bet of $36 (or 36 per cent).
By Peter Travers
PRACTICAL PUNTING - OCTOBER 1991