Many attest that there are some fundamental principles in gambling, just as there are for life as a whole.
For instance, as there are no exceptions to the law of gravity in physics, there are also similar laws in gambling that are equally absolute. The gambling principles I refer to are mathematical and are as true today as they were when the first horse was run.
While I have in the past and continue to argue that it is possible to “tweak” mathematics somewhat to turn some small negative situations into the positive, in essence it is not a preferred option as invariably the risks of losing increase accordingly.
In their classic book Dr. Z’s Beat The Racetrack, William Ziemba and Donald Hausch set down what they consider to be the desirable elements of a money management (staking) plan. These guidelines are:
- Current betting wealth (betting bank) should influence bet size – that is, as the bankroll increases so should, on average, bet size;
- The likelihood of winning should influence bet size;
- The “edge” – that is the measure of the difference between the estimate of the likelihood of winning and the public’s estimate translated into return per dollar bet, should also influence bet size; and
- The trade-off between betting bank growth and its security needs to be considered.
The reality is that very few staking plans meet all if any of those criteria. Notwithstanding, they are ideals that should be attempted to be met.
Over the next two parts of this series, I will be putting to the test a number of staking plans against the same set of results in what I’ve termed the Practical Punting Monthly Staking Plan Challenge.
The selections chosen to test the various staking plans come from one of the finest form analysts I know of, someone with a proven record of achievement.
Stuart Mackay is a Melbourne based form analyst who specialises in Perth racing. Stuart uses the pseudonym “The King Of Belmont” and he provides selections for all Perth meetings, including the mid-weeks.
Making selections in each race, he also nominates a “best bet” and it is these that will be the “testing material” for the staking plans.
As this article is being written, Stuart’s statistics for his best bets from January 1 2003 up until October 28 2004, which provide a steady stream of winners with a good strike rate and no real long losing runs, can be found in
Table 1.
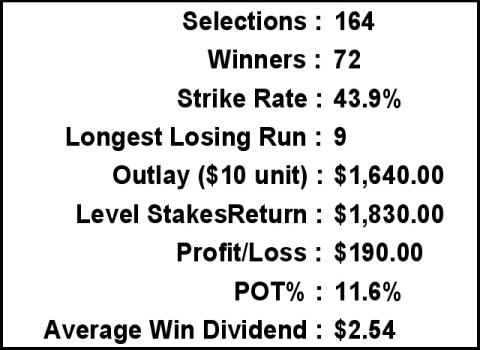
TABLE 1
The first of the staking plans tested is described as a conservative plan, one designed to moderately increase the stakes without creating problems.
The simple to understand rules are:
- Bet level stakes, increasing the original stake by 10 per cent after a winner; and
- Never regress the staking level.
This approach may appear tame, but it is a classic example of living to fight another day and in this regard remains relatively safe. This staking plan takes no notice of the increase in the bank: it requires that there simply has to be one.
If, for example, you commence with a bank of $1,000 and an initial bet of $10, you remain on the bet of $10 until you strike a winner before recalculating the stake for the next bet, which should be $11. You never regress, but you must wait for the next winner before increasing the stake by another 10 per cent of your original stake, that is to say, by another $1.
You are only increasing your bets by 1/10 after each winner – that is 1/10 of your commencing stake.
Ten winners will see an increase from one full staking unit to two full staking units. So the progression is quite moderate and only comes after the previous bet has been successful.
In accordance with the example above, commencing with a betting bank of $1,000 an initial bet of $10, just how this staking plan panned out can be found in Table 2.
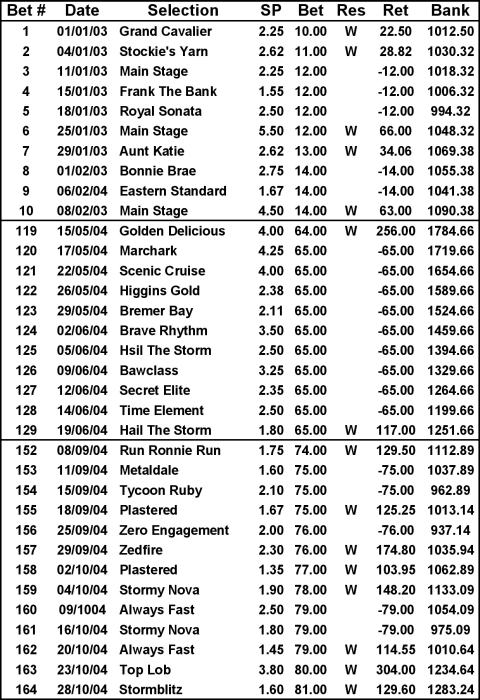
TABLE 2
Just a slice of the selections have been shown: the first 10, followed by the section that contains the longest losing run and then the last 13 (to date).
When measured against the level stakes performance this staking plan fails as on a turnover of $7,696, the profit of $283.24 represents a Profit on Turnover (POT) of just 3.7 per cent, some 7.9 per cent less.
During the longest losing run, with the bet size stuck on $65, the betting bank dropped by a whopping $585 or 58.5 per cent of the starting bank!
The next staking plan considered is described as being:
- Extremely safe;
- Continuously profitable;
- Flexible enough to be adapted to most requirements; and
- Easy to operate and monitor.
- The rules are:
- Set profit level requirement (which is indicated as a percentage of return of investment);
- Commencing with a basic unit investment, progress up the scale only when the predetermined profit level is not being achieved; and
- The progression scale is based on the profit level requirement.
Based on a $5 base unit and a 20 per cent profit level requirement, the progression scale in Table 3 has been used in the test.
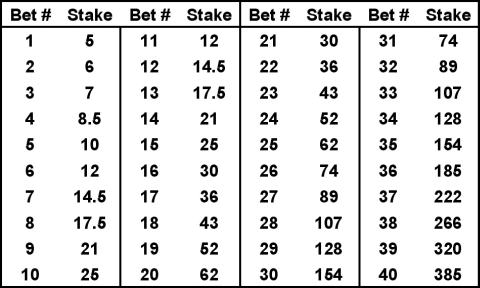
TABLE 3
The results so far are interesting and Table 4 contains the first 10 and the last 23 selections (to date).
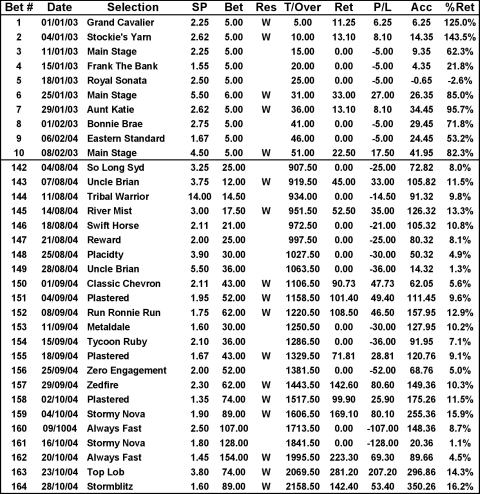
TABLE 4
While there is an overall improvement in the POT, it does come at an unacceptable cost in terms of bet size, with the largest bet so far being $154 which equates to over 30 times the base bet. As well, there are times, such as bet #161, when the profit level fell well below the level stakes achievement, which adds to the unacceptability of this staking plan when chasing a 20 per cent target.
However, when a somewhat less ambitious profit level is set there are some dramatic changes in bet size. For instance, a 10 per cent target results in a maximum bet of only $6, the downside being that the outcome hardly differs from the level stakes achievement.
This staking plan is subject to severe swing changes in performance as bets #159 to #164 indicate.
In the next part of this series, more staking plans will be put to the test, of which at least one will meet and better the level stakes performance without the stresses of large stake sizes or huge swings in performance.
Click here to read Part 2.
By EJ Minnis
PRACTICAL PUNTING - DECEMBER 2004