In this article, our senior contributor EJ Minnis replies to queries sent in by PPM readers. Please send any questions to: The Editor, PPM, PO Box 551, Dee Why, NSW 2099.
"Just writing to thank you all at Practical Punting Monthly for your Punters Comp, which is terrific and has been a real help to me when betting at home on a Saturday afternoon using my TAB account. However, I sometimes go down to my local PubTab or Tabaret and want to know if you have a 'simple' formula that I can use with a hand-held calculator on such occasions?" asks Rae Stephenson from an outer Melbourne suburb.
The Punters Comp is a very useful program for those who want to bet multiple selections in a race. However, it does require users to have ready access to a computer and as you mentioned, Rae, there are times when this is not possible.
The method that follows is an ideal alternative that can be used either with pen and paper or with pen, paper and a hand-held calculator - it is not a selection method and is not intended to be so.
Once you have determined your selections, the staking strategy can then be used for working out the bet sizes on each of those selections.
The formula that I describe uses the principle that the shortest-priced selection will be backed as a "saver" bet - one that reclaims your overall outlay should it win - and all the other selections will be backed to return a profit, for at least a 50 per cent return on your total outlay, provided one of them is successful.
It is worth pointing out that this method will not work on every race and is best suited to races with an open market or one in which you are prepared to "take on" a short-priced favourite.
The greater the sum of the odds or dividends on offer, the greater the anticipated profit, so generally the method will not work where there are cramped markets with the odds on offer representing poor value.
THE DUTCH BOOK STAKING METHOD
- Determine the total amount of the stake (outlay).
- Work out the "saver" bet to enable the stake to be returned.
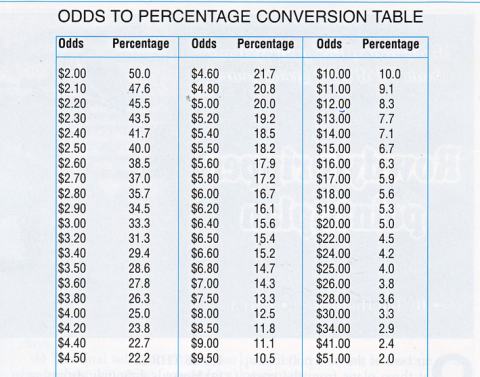
- Convert the other selections to percentages (using the odds to percentages chart on below).
- Deduct the "saver" bet from the total stake.
- Divide this amount by the sum of the percentages of the other selections.
- Multiply the individual percentages of the other selections by this factor.
The outcome of each of these multiplications is the bet size for each of the other selections.
Sound complicated? Well, yes, but in reality it's quite a simple process to work out. Let's work through a couple of examples.
Using the 2500m Piping Lane Handicap at Flemington in mid-February as the first example, the selections are the first four in the betting, It's Rysek, Heguy and Bold Bard with the favourite Palla Strozzi being the "saver" bet.
- $100 was determined as the total amount of the stake.
- Palla Strozzi was a $3.30 quote and therefore needed a $30 bet to return the total stake.
- It's Rysek was at $6, which converts to 16.7%; Heguy was at $6.50, which converts to 15.4%; and Bold Bard was at $8, which converts to 12.5%, for a total of 44.6%.
- Subtract the $30 bet on Palla Strozzi from the $100 total stake, which leaves $70 to bet on the other selections.
- Divide the $70 by 44.6 (the sum of the percentages of the other runners), equals 1.57, which is the multiplier.
- The bet sizes on the other selections were: It's Rysek $26 (16.7 x 1.57); Heguy $24 (15.4 x 1.57) and Bold Bard $20 (12.5 x 1.57).
The total of the bet-sizes were $30 + $26 + $24 + $20 = $100.
Heguy won and returned $156 ($24 by $6.50), for a profit of $56 or 56 per cent on the race.
What has to be determined is the minimum level of profit/return being sought and I would recommend that 50 per cent is the absolute limit, so the above example just fell within the minimum range in this regard.
Let's go through another example, one that offers a lot better value, but with some increase in risk. The HRC Plate, a black-type event for mares at Caulfield in early February, was a very open affair with two equal favourites at $4 but only four runners in the field of 13 at quotes of $10 or less.
Both favourites were coming back from a spell and could be risked, so the selections were the next four in the betting - Special Grange, Skewiff, Shaye Spice and Gold Lottey. Third favourite Special Grange, a mare that had never won second-up previously, had drawn the widest barrier and had a habit of getting back in her races, was used as the "saver" bet.
- Again $100 was determined as the total stake.
- Special Grange was at $4.80 and therefore needed a bet of $21 to return the total stake.
- Skewiff was at $10, which converts to 10%; Shaye Spice was at $15, which converts to 6.7%, and Cold Lottey was at $17, which converts to 5.9%, for a total of 22.6%.
- Subtract the $21 bet on Special Grange equals $79 of the $100 to bet on the other selections.
- Divide the $79 by 22.6 (the sum of the percentages of the other runners), equals 3.5, which is the multiplier.
- The bet sizes on the other selections were: Skewiff $35 (10 x 3.5); Shaye Spice $23.50 (6.7 x 3.5) and Cold Lottey $20.50 (5.9 x 3.5).
The total of the bet sizes were: $21 + $35 + $23.50 + $20.50 = $100.
In this race, Skewiff beat the fast finishing Special Grange, returning $350 for a profit of $250 or 250 per cent. It should be noted that while the profit was very good, the risk of losing the total stake was that much greater than in the example.
If the option of using a "saver" bet is not required, then simply disregard steps two and four of the six-point process, and determine the sum of the percentages (as per step 3) and the multiplier (as per step 5) by dividing the percentages sum into 100.
In the example of the HRC Plate, the multiplier would have been 2.3 with the bet sizes being as follows: Special Grange $48, Skewiff $23, Shaye Spice $15.50 and Cold Lottey $13.50, which would have returned only $230, but would have also given an additional opportunity of profiting on the race had Special Grange won.
For readers who haven't got their copy of Punters Comp, they can do so by visiting Australia's leading racing website, the Practical Punting Daily website at http://www.practicalpunting.com.au and downloading the free software program.
"I've been intrigued for a long time by the Fibonacci numbers and their role in gambling. Who was Fibonacci and why are his 'numbers' so important? " writes Peter Hartwell via email.
The history of numbers as we now know them in the western world can be traced back to 1202, when King John was in his third year on the throne of England, when the book Liber Abaci (The Book of the Abacus) was (hand) written in Italy.
The book contained fifteen chapters and was written by Leonardo Pisano (Leonardo of Pisa) who was aged about thirty at the time. Leonardo, better known today as Fibonacci, was the son of Bonacio, who was a consul in Pisa.
Bonacio translates as simpleton, while Fibonacci translates as blockhead. In either case, the terms seem totally inappropriate as Bonacio was apparently is well-respected consul to many courts, while his son was anything but a blockhead.
Liber Abaci was an extraordinary book by any standard as it made people aware of a whole new world in which numbers could be substituted for Hebrew, Creek and Roman systems that used letters for counting and calculating.
Such was the scope of the mathematics Fibonacci wrote about, that it was possible to calculate amongst other things interest rates and profit margins.
Fibonacci is best known for a short passage in Liber Abaci that led to something of a mathematical miracle. The passage concerns the problem of calculating how many rabbits will be born in the course of a year from just one pair of rabbits, assuming that every month each pair produces another pair and that rabbits begin to breed when they are two months old.
Fibonacci discovered that the original pair of rabbits would have spawned a total of 233 pair of offspring in the course of twelve months.
As at the end of each month the total number of rabbits would be as follows: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and 233, with each successive number being the sum of the two preceding numbers and it is this simple formula that has become known as the "Fibonacci numbers".
Divide any of the Fibonacci numbers by the next highest number and after 3 the answer is always 0.625; after 89 the answer is always 0.618. Divide any number by its preceding number and after 2, the answer is always 1.6; after 144, the answer is always 1.618.
The Greeks called these proportions the "Golden Mean", which defines the proportions of the Parthenon, the shape of playing cards, the horizontal bar on Christian crosses to that of the vertical bar and, importantly, these numbers and proportions have been used by gamblers in various staking methods ever since being disclosed.
(Note: I am indebted for much of the information used in answering this question to that which is contained in the book Against The Gods by Peter L. Bernstein, published by John Wiley and Sons.)
By EJ Minnis
PRACTICAL PUNTING - APRIL 2003